Robust Synchronization for High Penetration of Inverter Based Resources
Written by Chao Wu, Subham Sahoo, and Frede Blaabjerg
To achieve the goal of carbon free energy infrastructure as soon as possible, an extensive development and installation of renewable energy such as wind and solar is imperative. The way that renewable energy is converted into electrical energy is different than traditional thermal power generation. It is not based on synchronous generators, but has transitioned to a system dominated with power electronic converters. Thus, these renewable energy resources are generally called inverter-based resources (IBRs). The large-scale development of wind and solar power will inevitably lead to significant changes in the power system, that is, a transition from a synchronous generator-based power system to a power electronic converter-based system as shown in Fig. 1. This transition will also bring a series of emerging problems, such as the decrease in grid strength and low inertia of the grid, which will make it difficult to maintain the voltage and frequency stability. One of the important questions of such a modern power system is how to achieve a robust synchronization of multiple distributed IBRs. Different from the conventional synchronous generator, which is based on the inherent 'swing equation' guaranteeing the synchronization with the grid, IBRs’ synchronization is based on the implemented control strategies for maintaining the synchronization. The general control structure of IBRs is shown in Fig. 2. The effect of different control levels on the synchronization performance will be discussed.
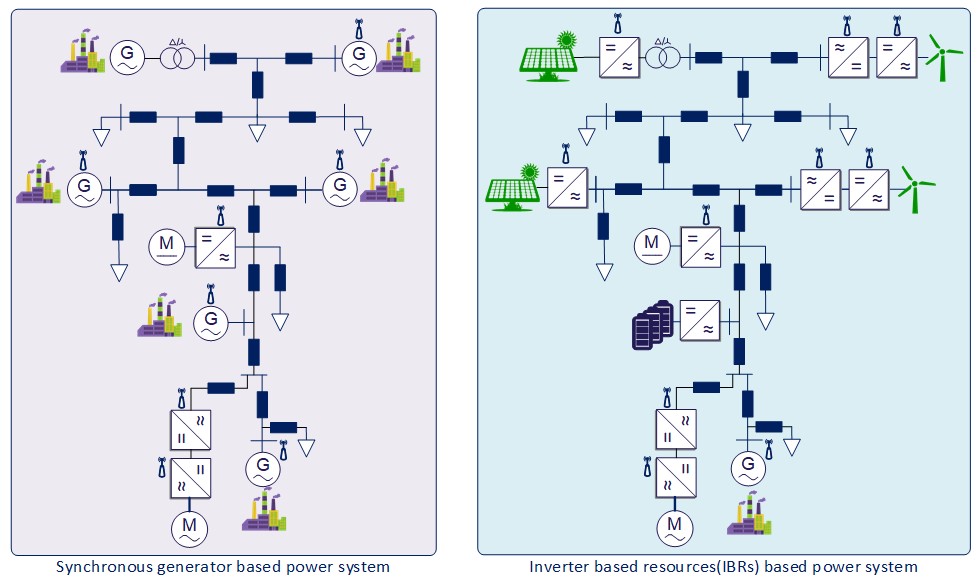
Fig.1. The transition from conventional power based power system to IBRs based power system
In secondary control, the power reference of each IBR is generated at this level, which has a significant effect on the synchronization stability. The information and communication technologies play a vital role in enhancing the synchronization performance of the IBRs based power system. Furthermore, such a large-scale integration and monitoring of IBRs needs significant efforts in terms of sensing and acquisition, where supervisory control and data acquisition (SCADA) systems are usually employed. However, these functionalities also increase the vulnerability to cyber risks and adversarial intrusions. The cyber attacks might change the power reference, which will affect the synchronization performance of each IBR. Considerable methods to avoid this practice can be achieved in a stepwise manner. First, cyber attacks should clearly be differentiated from any system faults. Once this step is accomplished, a diagnosis of the presence of cyber attack in the affected components needs to be carried out. Finally, once the compromised component is detected, the attack source is removed from the system. A good measure of IBR resiliency can be given by how quickly the IBR is restored to its normal operation following a cyber attack. As a result, further investigation needs to be carried out on identifying the risky sectors in the cyber layer equipped with control of IBRs.
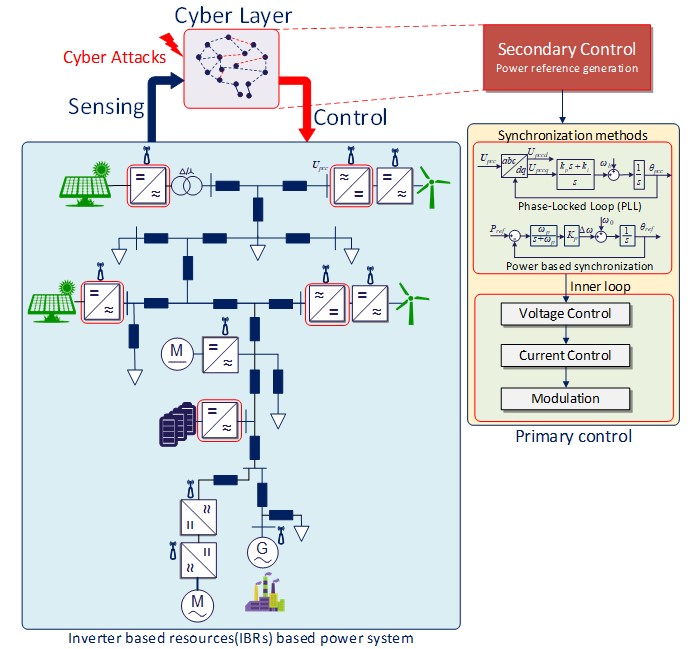
Fig. 2. General control structures of inverter-based resources (IBRs)
In the primary control of IBRs, there are two different synchronization methods: grid-following control and grid forming control. In the grid following control, the phase-locked loop (PLL) is applied for obtaining the phase and frequency of the voltage at the point of common coupling (PCC). These synchronization method works well under strong grid condition. However, due to the high ratio of IBRs integrated to the grid, the short circuit ratio (SCR) becomes smaller, which causes the PCC voltage fluctuataions against the output power of IBRs. Under this situation, it has been proved that there is a negative resistance introduced by the PLL, which causes instability and limits the power transfer of IBRs in low SCR grids. To overcome aforementioned problems, grid forming control methods are proposed. A wide variety of grid forming control schemes has been developed for IBRs, such as power synchronization control, droop control, virtual synchronous generator, synchronverter, and so on. Generally speaking, all these methods are based on power synchronization, which means that the control angle of the IBRs coming from the power control loop. This is a big difference from the PLL based method, which is based on voltage synchronization. This obvious synchronization difference ensures that the grid forming control can perform well under low SCR grid and even in standalone mode.
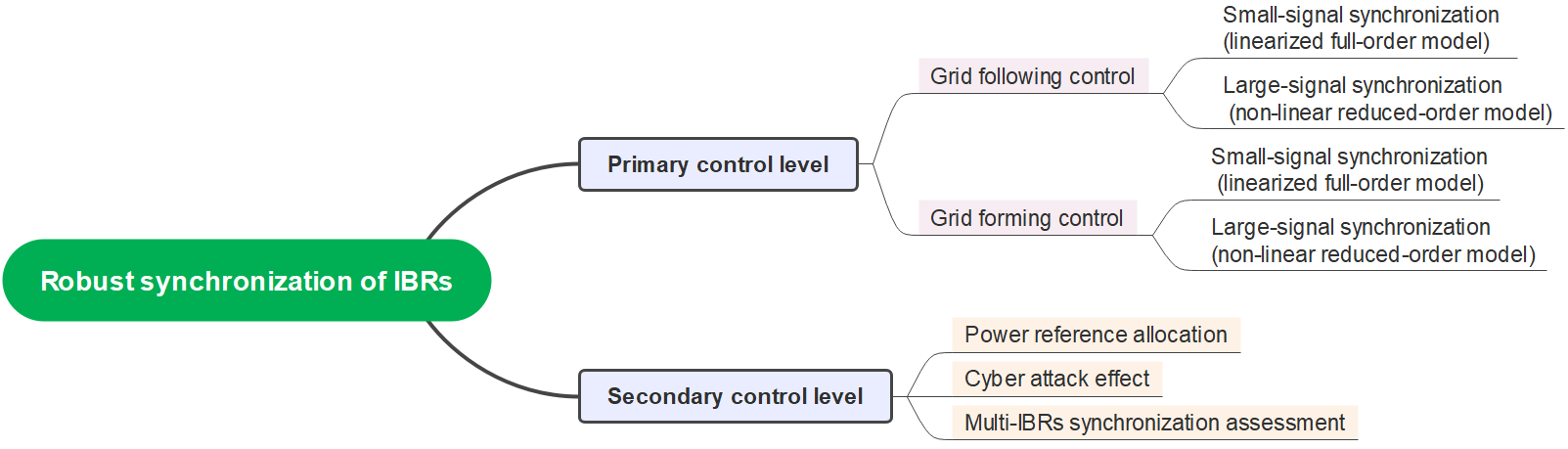
Fig. 3. Robust synchronization of IBRs from different control levels.
Furthermore, synchronization stability should also be guaranteed during large disturbances like grid faults, sudden generation/load loss or SCR change. The IBRs should also keep synchronized with the main grid during these large disturbances to support the grid instead of direct trip. Since the synchronization blocks, whether is voltage-based PLL or power-based synchronization methods, are all non-linear links. Modelling of these non-linear blocks is a big challenge, while also considering the cascaded inner control loops. Some classical non-linear analysis methods, such as phase-plane analysis, energy function, or Lyapunov-based methods can be used for analyzing such kind of synchronization issues.
To achieve a robust synchronization of IBRs, all different control levels should be considered shown as Fig. 3. In the secondary control level, the synchronization should be guaranteed to resist the cyber-attack. The equilibrium point can be maintained by an accurate power allocation of different IBRs during the grid faults or other kinds of large disturbances. In the primary control, the small-signal synchronization stability should be ensured first through a good design of the synchronization parameters under weak grid. In order to avoid the effect of inner voltage or current control loop on the synchronization performance, an obvious bandwidth difference of different control loops is essential for the generalized parameter design of IBRs. In this way, the synchronization issues can be decoupled from inner loops by arranging in different time scales. During this process, the H∞ method can be applied for considering the grid uncertainty and disturbances. Then, the reduced-order non-linear model can be used for the large-signal synchronization analysis. Furthermore, how to build the model of multi-IBRs based on hybrid synchronization methods (grid-following and grid-forming) when assessing the synchronization stability of the system is also an open question. The Kuramoto model might be a good solution for analyzing the synchronization stability of the multi-converter system.
This article edited by Mehmet Cintuglu
For a downloadable copy of the June 2021 eNewsletter which includes this article, please visit the IEEE Smart Grid Resource Center.



To have the Bulletin delivered monthly to your inbox, join the IEEE Smart Grid Community.
Past Issues
To view archived articles, and issues, which deliver rich insight into the forces shaping the future of the smart grid. Older Bulletins (formerly eNewsletter) can be found here. To download full issues, visit the publications section of the IEEE Smart Grid Resource Center.




