Energy Storage Systems Applications in Mexican Power System
By Jorge L. Angarita, Jorge Martínez-Crespo, and Ameena Al Sumaiti
Introduction
The Energy Storage Systems (ESS) -hydro pumping stations and battery systems, for example- are becoming a realistic alternative to act in the wholesale markets as any other participant, i.e. generators, consumers or prosumers. The increasing interest in ESS for the grid can be due to multiple factors, amongst others, the progressive integration of renewable energy sources, the high capital costs of handling peak demands or the investments required for the improvement of the grid reliability.
This article poses a model to calculate the revenue streams of ESS (batteries) in the Mexican electricity pool market. The model considers revenues from energy trading as a result of buying energy at a low price and selling it at a higher price acting in a day-ahead market (DAM). Another revenue stream could come from selling capacity or ancillary services, but this type of revenue is not considered here.
The Mexican Wholesale Electricity Market
The Mexican energy market began in 2016 after an unbundling process and the subsequent creation of an open market. According to the market rules, all the agents must send their energy-price bids on hourly basis. These bids shall be submitted to the Market Operator (MO), CENACE , and shall be included in a matching procedure effective for the day-ahead scheduling horizon, corresponding to the day D following the market session (day D-1).
In the Mexican day-ahead market, there is not a single marginal price but rather several Local Marginal Prices (LMP) or nodal prices, where some of them represent the behavior of an area where aggregating the demand. The LMP are calculated in each node i of the system based on 3 components: energy, congestion and losses.
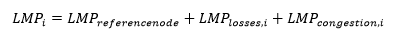
The price should capture –in addition to the marginal cost of generating electricity– economic signals that indicate how saturated the system networks are, as well as the level of transmission losses.
Therefore, since there is a number of nodal prices, physical or virtual, the performance of the ESS will be conditioned by the node where it is located.
EES Model for the Mexican Wholesale Market
The ESS self-schedule model should portray the arbitrage process in the Mexican day-ahead electricity market. The aim of the self-schedule model will be, therefore, to define how much energy should be bid to the DAM and the price of this energy bid, that is, the price is willing to pay/receive for the energy bought from/sold to the market. Moreover, the ESS self-schedule models should internalize both the technical and financial parameters to make the bid feasible whilst looking for profit. It is well-known that the energy prices paid to the players in the wholesale markets are not known before the settlement process. The matching process takes into account bids from generators and offers from consumers and defines which bids and offers were accepted and the marginal price paid to all winner participants. Usually the goal of the market is to maximize the system social welfare, i.e. the generator and consumer surplus in the market equilibrium.
Therefore, accordingly with the process described, the market players must evaluate their bids using an estimation of the expected price of day D as an input to the model. Using prices forecasting algorithms, the player can decide its better bid: the optimal amount of energy and the price. Finally, to assess the quality of the described decision process, it is necessary to compare the obtained results with the maximum theorical profit, which would be obtained with perfect forecasting. The difference between these two processes is the improvement gap, whose value is mainly associated with the precision of the price forecasting. Hence the decision process of the EES model (see Fig. 1) is made of three consecutive steps: price forecasting, ex-ante decision process and results evaluation.
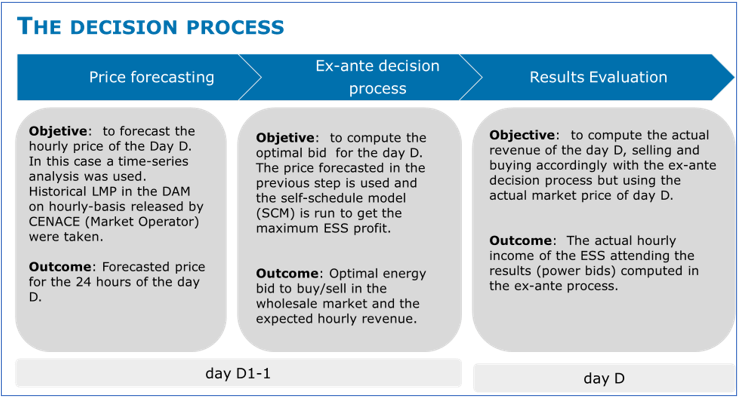
Fig. 1 The Decision Process
The self-schedule ESS model implemented considers the ESS as a price-taker agent, that is to say, its participation will not change the actual market price because of its relatively small size. Likewise, as any mathematical optimization model, the self-scheduling ESS model are made of multiple variable and parameters that define the objective function and the constraints to be fulfilled. Next, we describe the objective function, the parameters and the constraints:
- The objective function is the net daily income, i.e. hourly sum of the income from selling energy (hourly energy delivered times the hourly local marginal price) minus the payments (hourly energy taken times the hourly local marginal price).
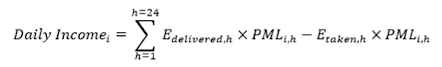
- The main constraints of the models are:
- Hourly energy balance: The hourly energy storage (Eh) is the energy storage during the hour before (Eh-1) plus the energy transaction during hour h (Eth) minus the charging energy losses (Lossh).
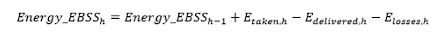
-
- Hourly maximum energy delivery, which is defined by the capacity of the inverters.

-
- Maximum energy storage capacity stated by the battery’s capacity.
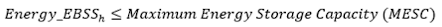
- The model contains multiple parameters (maximum hourly energy production, maximum energy storage, charging and discharging ESS efficiency) and other input information as the expected hourly market price. This model was implemented in an optimization software tool (General Algebraic Modeling System GAMS) as a Mix Integer Linear Problem (MILP).
- The main results obtained after running the model are:
- Hourly energy to be bought/sold during the day D in the day-ahead market.
- Expected hourly revenue along the day D in the day-ahead market.
Results
Table 1 shows the three different scenarios analyzed which take into account different Maximum Energy Storage Capacity (MESC) and Maximum Hourly Delivery Capacity (MHDC).
Table 1 Energy Scenarios

The simulations consider a simulation period of six months (January-June 2019). Fig. 2 shows the revenue for 8 different price zones (LMP) in the Mexican wholesale market. The values represent only those revenue obtained from the energy matching process. Additional revenue from selling power capacity and ancillary services should also be added.
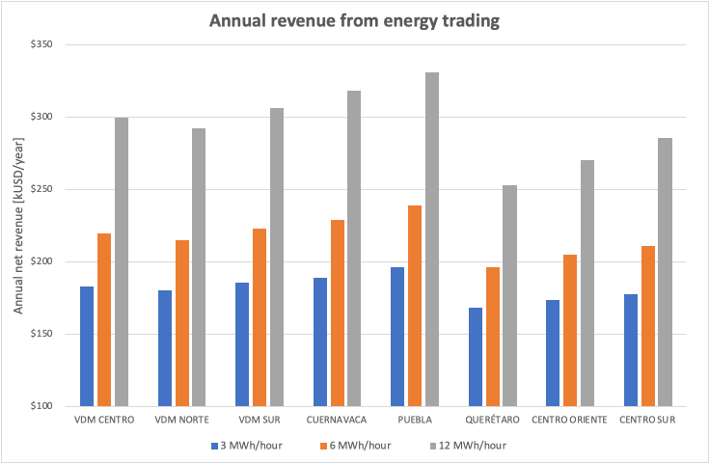
Fig. 2 Annual revenue from energy trading
There are relevant differences in the profitability of the ESS depending on the location because of the differences in nodal LMP. For example, the revenue in Puebla is 17%, 12% and 31% higher than the revenue in Querétaro for scenarios 1-2-3, respectively. The MHDC of the ESS restricts the revenue in a very significant way. If the case of Puebla node is analyzed, the MHDC of scenarios 2 and 3 provides 21.86% and 68.68%, respectively, higher revenue than the MHDC of scenario 1. Finally, it is carried out a sensitivity analysis of the optimal ratio of the battery size versus the inverter size, i.e. MESC/MHDC. Table 2 shows the annual revenue in $USD for different price zones and four different MESC values. The MHDC considered is 3 MWh/hour.
Table 2. Annual revenue (kUSD/year)

The results show that the higher the storage capacity (MESC) is, the greater the revenue is, since the ESS can store more energy to sell it later at a higher price. However, it is not always profitable enough to increase the battery capacity, for example, considering the Puebla prices, having 4 times more storage capacity, i.e. from 3 MWh to 12 MWh, the increase in the annual revenue is only 16.76%, which does not look profitable. Therefore, it is clear that it would be necessary to define the optimal ratio MESC/MHDC.
Conclusion and Final Discussion
The benefit of the ESS is mainly driven by the difference between the valley and peak period prices. Despite the ESS was considered as a price taker, it actually changed the prices profile making it flatter. The ESS behaves as an additional demand in the valley price, raising the price, and conversely, as a seller in the peak period reducing the prices. This effect should be modelled carefully to make a right assessment of the ESS impact on the whole system and market players.
In order to make an optimal investment, the investor should define the optimal ratio between MESC and MHCD, either using shadow prices of the associated constraints of the model or including these parameters (MESC and MHCD) as variables in the model.
Final Discussion (bid-based vs cost-based markets)
The Mexican wholesale market began almost four years ago, therefore, it is a relatively new market still making adjustments. In order to avoid price control of the main dominant players, a cost-based system was enforced and so, the energy sellers should offer their incremental energy cost defined by the cost function (hill-chart or the incremental heat-rate). In fact, it is an effective method to prevent price-maker positions. However, it is relevant to consider whether it is necessary or convenient to move towards a bid-based market where players can bid the energy and price they consider the best. It is particularly relevant when agents like ESS are contemplating to get into the market and their decisions are mainly driven by the market price.
For a downloadable copy of April 2020 eNewsletter which includes this article, please visit the IEEE Smart Grid Resource Center.

Jorge Martínez-Crespo received a B.Sc. degree in power engineering from E.T.S. de Ingenieros Industriales de Madrid, Spain, in 1995 and the Ph.D. degree in electrical engineering from Universidad Carlos III de Madrid, Spain, in 2004. In 1998, he joined the Department of Electrical Engineering at the Universidad Carlos III de Madrid. His research interests include power systems operation, planning, and optimization, energy economics and energy education.
Ameena Saad Al-Sumaiti received a B.Sc. degree in electrical engineering from United Arab Emirates University, United Arab Emirates, in 2008, and the M.Sc. and Ph.D. degrees in electrical and computer engineering from the University of Waterloo, Canada, in 2010 and 2015, respectively. She was a Visiting Assistant Professor with MIT, Cambridge, MA, USA, in 2017. She is currently an Assistant Professor with the Department of Electrical Engineering and Computer Science, Khalifa University, Abu Dhabi, United Arab Emirates. Her research interest includes intelligent systems, energy policy, and economics.
To have the Bulletin delivered monthly to your inbox, join the IEEE Smart Grid Community.
Past Issues
To view archived articles, and issues, which deliver rich insight into the forces shaping the future of the smart grid. Older Bulletins (formerly eNewsletter) can be found here. To download full issues, visit the publications section of the IEEE Smart Grid Resource Center.




